Draw a Circle of Radius 3.4 Cm and Centre E

Maharashtra Land Board Class 10 Maths Solutions Chapter 4 Geometric Constructions Trouble Set 4

Question 1.
Select the correct alternative for each of the following questions.

i. The number of tangents that tin can be drawn to a circle at a indicate on the circle is ______
(A) 3
(B) 2
(C) 1
(D) 0
Answer:
(C)

2. The maximum number of tangents that can exist drawn to a circumvolve from a bespeak outside information technology is ______
(A) 2
(B) 1
(C) 1 and but ane
(D) 0
Respond:
(A)

iii. If ∆ABC ~ ∆PQR and \(\frac { AB }{ PQ } \) = \(\frac { 7 }{ 5 } \), then ______
(A) AABC is bigger.
(B) APQR is bigger.
(C) both triangles will exist equal
(D) can not exist decided
Reply:
(A)

Question 2.
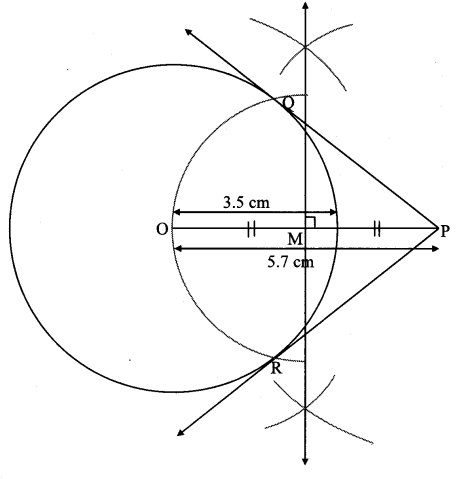
Depict a circle with eye O and radius 3.v cm. Take bespeak P at a distance five.7 cm from the centre. Draw tangents to the circumvolve from point P.
Solution:
Analysis:
Every bit shown in the figure, permit P be a point in the outside of circumvolve at a distance of 5.7 cm.
Let PQ and PR be the tangents to the circle at points Q and R respectively.
∴ seg OQ ⊥ tangent PQ …[Tangent is perpendicular to radius]
∴ ∠OQP = 90°

∴ bespeak Q is on the circle having OP every bit diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point R too lies on the circle having OP equally diameter.
∴ Points Q and R lie on the circle with OP as diameter.
On drawing a circle with OP as diameter, the points where information technology intersects the circle with center O, will exist the positions of points Q and R respectively.

Question 3.
Draw whatever circumvolve. Have whatsoever signal A on it and construct tangent at A without using the centre of the circumvolve.
Solution:
Analysis:
Equally shown in the figure, line l is a tangent to the circle at point A.
seg BA is a chord of the circle and ∠BCA is an inscribed angle.
By tangent secant bending theorem,
∠BCA = ∠BAR

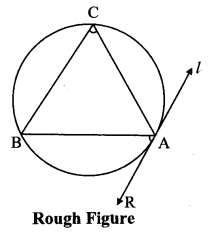
By converse of tangent secant angle theorem,
If nosotros depict ∠BAR such that ∠BAR = ∠BCA, and so ray AR (i.e. line fifty) is a tangent at point A.

Question four.
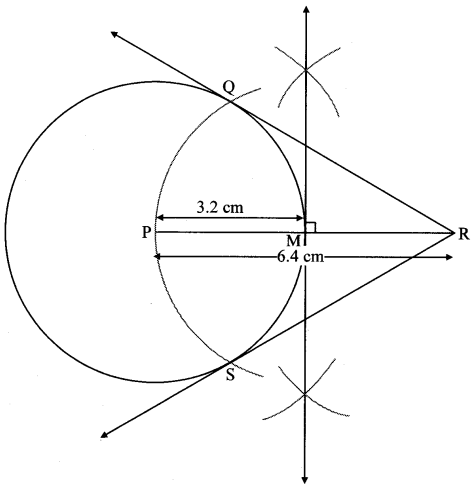
Draw a circle of bore 6.iv cm. Have a point R at a distance equal to its diameter from the eye. Draw tangents from indicate R.
Solution:
Diameter of circle = 6.4 cm 6.4
Radius of circle = \(\frac { 6.four }{ two } \) = iii.2 cm
Analysis:
As shown in the effigy, permit R be a point in the exterior of circumvolve at a altitude of 6.4 cm.
Let RQ and RS be the tangents to the circle at points Q and Due south respectively.

∴ seg PQ ⊥tangent RQ …[Tangent is perpendicular to radius]
∴ ∠PQR = 90°
∴ point Q is on the circle having PR as diameter. …[Angle inscribed in a semicircle is a right bending]
Similarly,
Point South also lies on the circumvolve having PR every bit bore.
∴ Points Q and S lie on the circle with PR equally diameter.
On drawing a circle with PR as bore, the points where it intersects the circle with centre P, volition exist the positions of points Q and Southward respectively.

Question 5.
Describe a circle with centre P. Draw an arc AB of 100° measure. Draw tangents to the circle at point A and point B.
Solution:
m(arc AB) = ∠APB = 100°
Analysis:
seg PA ⊥ line l
seg PB ⊥line m … [Tangent is perpendicular to radius]

The perpendicular to seg PA and seg Pb at points A and B respectively will requite the required tangents at A and B.

Steps of construction:
i. With centre P, draw a circle of any radius and take any indicate A on it.
ii. Draw ray PA.
iii. Draw ray PB such that ∠APB = 100°.
iv. Describe line 50 ⊥ray PA at bespeak A.
v. Draw line m ⊥ ray Atomic number 82 at point B.
Lines l and 1000 are tangents at points A and B to the circumvolve.

Question vi.
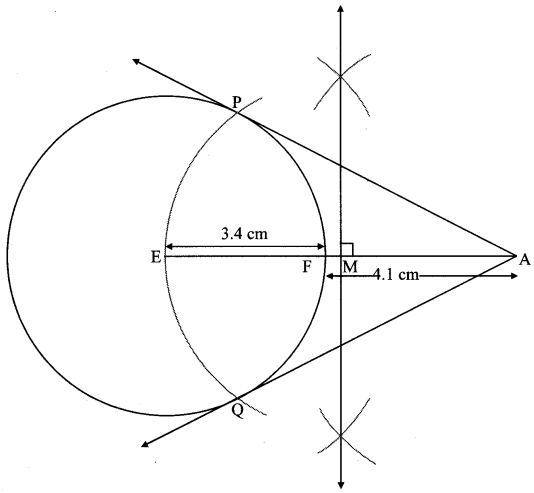
Describe a circle of radius three.iv cm and centre E. Take a point F on the circle. Take another bespeak A such that East – F – A and FA = four.1 cm. Draw tangents to the circle from bespeak A.
Solution:
Analysis:
Draw a circle of radius three.4 cm
As shown in the figure, let A be a signal in the outside of circle at a distance of (3.4 + 4.1) = vii.five cm.
Let AP and AQ be the tangents to the circle at points P and Q respectively.
∴ seg EP ⊥ tangent PA … [Tangent is perpendicular to radius]

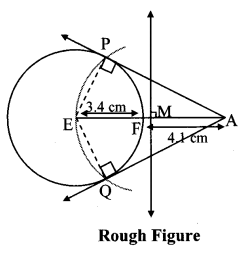
∴ ∠EPA = xc°
∴ point P is on the circle having EA equally diameter. …[Bending inscribed in a semicircle is a correct angle]
Similarly, point Q likewise lies on the circle having EA as bore.
∴ Points P and Q lie on the circumvolve with EA as bore.
On drawing a circle with EA as diameter, the points where information technology intersects the circumvolve with centre Due east, will be the positions of points P and Q respectively.

Question 7.
∆ABC ~ ∆LBN. In ∆ABC, AB = five.one cm, ∠B = 40°, BC = four.8 cm, \(\frac { AC }{ LN } \) = \(\frac { iv }{ 7 } \). Construct ∆ABC and ∆LBN.
Solution:
Assay:
As shown in the figure,
Let B – C – N and B – A – L.

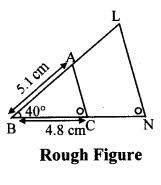
∆ABC ~ ∆LBN …[Given]
∴ ∠ABC ≅ ∠LBN …[Respective angles of similar triangles]
\(\frac { AB }{ LB } \) = \(\frac { BC }{ BN } \) = \(\frac { AC }{ LN } \) …(i)[Corresponding sides of similar triangles]
But. \(\frac { Air-conditioning }{ LN } \) = \(\frac { 4 }{ 7 } \) …(ii)[Given]
∴ \(\frac { AB }{ LB } \) = \(\frac { BC }{ BN } \) = \(\frac { Ac }{ LN } \) = \(\frac { 4 }{ seven } \) …[From(i)and(two)]
∴ sides of ∆LBN are longer than corresponding sides of ∆ABC.
∴ If seg BC is divided into four equal parts, so seg BN will be 7 times each office of seg BC.
So, if we construct ∆ABC, bespeak N volition be on side BC, at a distance equal to 7 parts from B.
Now, signal 50 is the point of intersection of ray BA and a line through Northward, parallel to AC.
∆LBN is the required triangle similar to ∆ABC.

Steps of construction:
i. Depict ∆ABC of given measure. Describe ray BD making an acute angle with side BC.
2. Taking convenient distance on compass, marking seven points B_i, B_two, B₃, B₄, B₅, B₆ and B₇ such that
BB₁ = B₁B₂ = B_iiB₃ B₃= B4_four = B₄B₅ = B_vB₆ = B_half-dozenB_seven.
iii. Join B₄C. Draw line parallel to B_fourC through B_seven to intersects ray BC at N.
iv. Draw a line parallel to side AC through Due north. Name the point of intersection of this line and ray BA as Fifty.
∆LBN is the required triangle similar to ∆ABC.

Question eight.
Construct ∆PYQ such that, PY = six.3 cm, YQ = seven.2 cm, PQ = v.viii cm. If = \(\frac { YZ }{ YQ } \) = \(\frac { 6 }{ five } \) then construct ∆XYZ similar to ∆PYQ.
Solution:

Assay:
As shown in the figure,
Let Y – Q – Z and Y – P – Ten.
∆XYZ ~ ∆PYQ …[Given]
∴ ∠XYZ ≅ ∠PYQ …[Corresponding angles of like triangles]
\(\frac { XY }{ PY } \) = \(\frac { YZ }{ YQ } \) = \(\frac { XZ }{ PQ } \) …(i)[Respective sides of like triangles]
Merely, \(\frac { YZ }{ YQ } \) = \(\frac { 6 }{ 5 } \) ,..(two)[Given]
∴ \(\frac { XY }{ PY } \) = \(\frac { YZ }{ YQ } \) = \(\frac { XZ }{ PQ } \) = \(\frac { 6 }{ 5 } \) …[From (i) and (ii)]
∴ sides of ∆XYZ are longer than corresponding sides of ∆PYQ.
∴ If seg YQ is divided into five equal parts, and then seg YZ volition be 6 times each part of seg YQ.
So, if nosotros construct ∆PYQ, point Z will exist on side YQ, at a distance equal to 6 parts from Y.
Now, point X is the betoken of intersection of ray YP and a line through Z, parallel to PQ.
∆XYZ is the required triangle similar to ∆PYQ.

Steps of structure:
i. Draw ∆ PYQ of given measure. Describe ray YT making an astute bending with side YQ.
ii. Taking convenient distance on compass, mark 6 points Y₁, Y₂, Y₃, Y₄, Y_v and Y_half-dozen such that
YY_ane = Y₁Y_ii = Y_iiY_iii = Y₃Y_four = Y_fourY_v = Y₅Y₆.
iii. Join Y₅Q. Draw line parallel to Y₅Q through Y_{half dozen} to intersects ray YQ at Z.
iv. Draw a line parallel to side PQ through Z. Name the point of intersection of this line and ray YP as X.
∆XYZ is the required triangle like to ∆PYQ.

Maharashtra Board Form 10 Maths Solutions

vigilbutiffely.blogspot.com

Source: https://www.learncram.com/maharashtra-board/class-10-maths-solutions-part-2-chapter-4-problem-set-4/